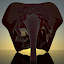
DigiTale: 3D Painting
Marjan Colletti (2005).
Marjan Colletti (2005).
I would like to investigate the rather paint like, malleable, dense, oozy, more workable digital materiality of intrafaces. CAD here works with substance that compares to a paint-body hybrid. It can be applied, stretched, but also cut, covered, sliced. Located somewhere between painting and photography, magic and surgery, the digital architect can manipulate and reveal properties of digital substance by creatively using software commands. [...]
Within CAD software environments, ‘lofts’ are complex surfaces that pass through a series of curves, enabling the creation of open or closed entities. Lofting builds upon the tradition of Surrealist ‘psychic automatism’, Gigeresque biomechanoid airbrushing, Miriam Cabessa’s body paintings and Roy Lichtenstein’s dot matrix brush prints.
‘Periodic surfaces’i are closed surfaces (such as a cylindrical surface) that can be deformed without developing ‘kinks’. Kinks, in comparison to knots, or control points of a spline, split the curve into multiple curves, and allow sharp, unsmooth edges along the spline. For the reason that (CAD) splines flow vectorially through their sequences of control points, they are ‘by definition continuous multiplicities rather than discrete entities’,ii as stated by Lynn. Lynn describes multiplicities as a ‘continuous assemblage of heterogeneous singularities’, representing a collection of heterogeneous components – without being reducible to either the entity or the collection – that simultaneously displays ‘collective qualities of continuity and local qualities of heterogeneity’.iii The possibility of deformation of periodical surfaces into kink-free, smooth, fluid geometries oozing between splines conveys the notion of poetic automatism within the Baudrillardian idea of ‘absolute singularity’ with ‘infinite seriality’iv; also expressed by the (serial) splinear cuts resulting by ‘sectioning’ and ‘contouring’ NURBS surfaces and volumes. Under such circumstances the CAD-created series of sections allow complexity yet retain parameters of compatibility and continuity.
Within CAD software environments, ‘lofts’ are complex surfaces that pass through a series of curves, enabling the creation of open or closed entities. Lofting builds upon the tradition of Surrealist ‘psychic automatism’, Gigeresque biomechanoid airbrushing, Miriam Cabessa’s body paintings and Roy Lichtenstein’s dot matrix brush prints.
‘Periodic surfaces’i are closed surfaces (such as a cylindrical surface) that can be deformed without developing ‘kinks’. Kinks, in comparison to knots, or control points of a spline, split the curve into multiple curves, and allow sharp, unsmooth edges along the spline. For the reason that (CAD) splines flow vectorially through their sequences of control points, they are ‘by definition continuous multiplicities rather than discrete entities’,ii as stated by Lynn. Lynn describes multiplicities as a ‘continuous assemblage of heterogeneous singularities’, representing a collection of heterogeneous components – without being reducible to either the entity or the collection – that simultaneously displays ‘collective qualities of continuity and local qualities of heterogeneity’.iii The possibility of deformation of periodical surfaces into kink-free, smooth, fluid geometries oozing between splines conveys the notion of poetic automatism within the Baudrillardian idea of ‘absolute singularity’ with ‘infinite seriality’iv; also expressed by the (serial) splinear cuts resulting by ‘sectioning’ and ‘contouring’ NURBS surfaces and volumes. Under such circumstances the CAD-created series of sections allow complexity yet retain parameters of compatibility and continuity.
[Images: 3D digital paint: periodic surfaces, and bloboids, by Marjan Colletti (2001)].
All 3D CAD software packages allow different ways of displaying digital space, the most common being: in wireframe, shaded, rendered (OpenGL, Phong, etc.) and hidden mode. On-screen shaded or rendered views simplify and approximate existing interactions and relationships between geometries and entities, lights and colours, materials and textures, transparencies and shadows. Rendered pixel graphics of vector-based drawings, on the other hand, calculate and depict quantitative and qualitative data with detail. As in photography, in general, renderings present themselves as 2D projections of 3D spatial properties and volumetric entities of digital space, and as snapshots of spatial-temporal defined circumstances. As in a photographic process, volumes, lights, transparencies are captured through a device and developed on a picture frame – in photography on the negative film (or directly to photosensitive paper as in Polaroid), and in renderings on the screen (or directly to file). The following images show a random 3D spline that is swept along itself forming a surface, almost like dye painted by a brush, resulting in a (in itself closed) surface that conveys a 3D, volumetric presence. The NURBS surface, built up by a series of curves defining its geometry, is only visible as volumetric entity when shaded or rendered. NURBS entities are defined by control points that can be located outside the physical (albeit digital) boundaries of the object itself.
[Images: A 3D spline is revolved along itself, creating convoluted blebs. Wireframe, shaded and rendered views, by Marjan Colletti (2005)].
i Rhinoceros, copyright Robert McNeel & Associates.
ii Lynn, Animate Form, p 23
iii Ibid.
iv Baudrillard, The System of Objects, p 88.
v Rhinoceros, copyright Robert McNeel & Associates.
vi Andrew Benjamin (ed.), Complexity – Architecture / Art / Philosophy, Journal of Philosophy and the Visual Art (London: Academy Editions, 1995, no. 6) p 7. Within the general interpretation of complexity, as Andrew Benjamin writes, it is the ‘Cartesian heritage’ of complexity that identifies the possibility of the complex.
ii Lynn, Animate Form, p 23
iii Ibid.
iv Baudrillard, The System of Objects, p 88.
v Rhinoceros, copyright Robert McNeel & Associates.
vi Andrew Benjamin (ed.), Complexity – Architecture / Art / Philosophy, Journal of Philosophy and the Visual Art (London: Academy Editions, 1995, no. 6) p 7. Within the general interpretation of complexity, as Andrew Benjamin writes, it is the ‘Cartesian heritage’ of complexity that identifies the possibility of the complex.